§ 174. Интерференция света в тонких пленках

В природе часто можно наблюдать радуж­ное окрашивание тонких пленок (масля­ные пленки на воде, мыльные пузыри, оксидные пленки на металлах), возникаю­щее в результате интерференции света, отраженного двумя поверхностями пленки. Пусть на плоскопараллельную про­зрачную пленку с показателем преломле­ния n и толщиной d под углом i (рис. 249) падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке О луч разде­лится на два: частично отразится от верх­ней поверхности пленки, а частично пре­ломится. Преломленный луч, дойдя до точ­ки С, частично преломится в воздух (n₀=1), а частично отразится и пойдет к точке В. Здесь он опять частично отра­зится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом ('. Вышедшие из пленки лучи 1 и 2 когерент­ны, если оптическая разность их хода мала по сравнению с длиной когерентности па­дающей волны. Если на их пути поставить

собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы и дадут интерференционную кар­тину, которая определяется оптической разностью хода между интерферирующи­ми лучами.

Оптическая разность хода, возникаю­щая между двумя интерферирующими лу­чами от точки О до плоскости АВ,

D=n(ОС+СВ)-(ОА±l₀/2),

где показатель преломления окружающей пленку среды принят равным 1, а член ±l₀/2 обусловлен потерей полуволны при отражении света от границы раздела. Ес­ли n>n₀, то потеря полуволны произойдет в точке О и вышеупомянутый член будет иметь знак минус, если же n<n₀, то потеря полуволны произойдет в точке С и l₀/2 будет иметь знак плюс. Со­гласно рис.249, OC=CB=d/cosr, ОA=ОВsini=2dtgrsini. Учитывая для данного случая закон преломления sini=nsinr, получим

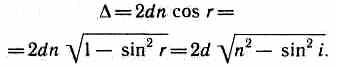
С учетом  потери полуволны для оптиче­ской разности хода получим

Для        случая,        изображенного        на рис. 249 (n>n₀),

В     точке     Р     будет     максимум,     если (см.(172.2))

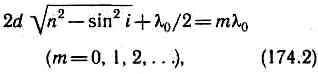
и минимум, если (см. (172.3))

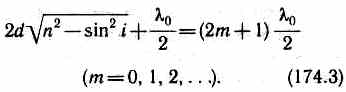
Доказывается, что интерференция наблю­дается только, если удвоенная толщина пластинки меньше длины когерентности падающей волны.

 

280

1. Полосы равного наклона (интерфе­ренция от плоскопараллельной пластин­ки). Из выражений (174.2) и (174.3) сле­дует, что интерференционная картина в плоскопараллельных пластинках (плен­ках) определяется величинами l₀, d, n и i. Для данных l₀, d и n каждому на­клону i лучей соответствует своя интер­ференционная полоса. Интерференцион­ные полосы, возникающие в результате наложения лучей, падающих на плоскопа­раллельную пластинку под одинаковыми углами, называются полосами равного на­клона.

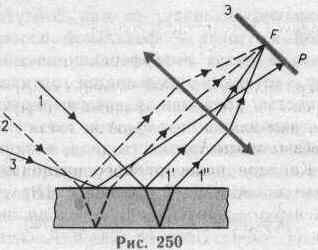
Лучи 1' и 1", отразившиеся от верхней и нижней граней пластинки (рис.250), параллельны друг другу, так как пластин­ка плоскопараллельна. Следовательно, ин­терферирующие лучи 1' и 1" «пересекают­ся» только в бесконечности, поэтому гово­рят, что полосы равного наклона локали­зованы в бесконечности. Для их на­блюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1" соберутся в фокусе F линзы (на рис. 250 ее оптическая ось параллельна лу­чам 1' и 1"), в эту же точку придут и дру­гие лучи (на рис.250 — луч 2), парал­лельные лучу 1, в результате чего увеличи­вается общая интенсивность. Лучи 3, наклоненные под другим углом, соберутся в другой точке Р фокальной плоскости линзы. Легко показать, что если оптиче­ская ось линзы перпендикулярна повер­хности пластинки, то полосы равного на­клона будут иметь вид концентрических колец с центром в фокусе линзы.

2. Полосы равной толщины (интерфе­ренция от пластинки переменной толщины).

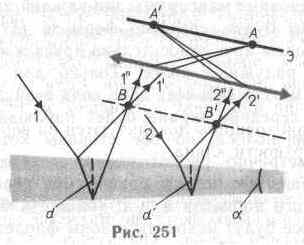
Пусть на клин (угол а между боковы­ми гранями мал) падает плоская волна, направление распространения которой со­впадает с параллельными лучами 1 и 2 (рис. 251). Из всех лучей, на которые разделяется падающий луч 1, рассмотрим лучи 1' и 1", отразившиеся от верхней и нижней поверхностей клина. При опре­деленном взаимном положении клина и линзы лучи 1' и 1" пересекутся в не­которой точке А, являющейся изображе­нием точки В. Так как лучи 1' и 1" коге­рентны, они будут интерферировать. Если источник расположен довольно далеко от поверхности клина и угол а достаточно мал, то оптическая разность хода между интерферирующими лучами 1' и 1" может быть с достаточной степенью точности вы­числена по формуле (174.1), где в качест­ве d берется толщина клина в месте паде­ния на него луча. Лучи 2' и 2", образо­вавшиеся за счет деления луча 2, падающего в другую точку клина, собираются линзой в точке А'. Оптическая разность хода уже определяется толщиной d'. Таким образом, на экране возникает система интерференционных полос. Каж­дая из полос возникает за счет отражения от мест пластинки, имеющих одинаковую толщину (в общем случае толщина пластинки может изменяться произволь­но). Интерференционные полосы, возника­ющие в результате интерференции от мест одинаковой толщины, называются полоса­ми равной толщины.

Так как верхняя и нижняя грани клина не параллельны между собой, то лучи 1' и 1" (2' и 2") пересекаются вблизи пластинки, в изображенном на рис. 251 случае — над ней (при другой

 

281

конфигурации клина они могут пересе­каться и под пластинкой). Таким образом, полосы равной толщины локализованы вблизи поверхности клина. Если свет па­дает на пластинку нормально, то полосы равной толщины локализуются на верхней поверхности клина.

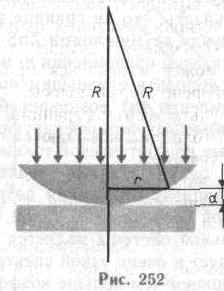
3. Кольца Ньютона. Кольца Ньютона, явля­ющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопа­раллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиу­сом кривизны (рис. 252). Параллельный пучок света падает нормально на плоскую повер­хность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора меж­ду линзой и пластинкой. При наложении отра­женных лучей возникают полосы равной толщи­ны, при нормальном падении света имеющие вид концентрических окружностей.

В отраженном свете оптическая разность хода (с учетом потери полуволны при отра­жении), согласно (174.1), при условии, что показатель преломления воздуха n=1, а i=0,

D=2d+l₀/2,

где d — ширина зазора. Из рис. 252 следует, что R²=(R-d)²+r², где R — радиус кривизны линзы, r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим d = r²/(2R). Следовательно,

D= r²/R+l₀/2. (174.4)

Приравняв (174.4) к условиям максимума (172.2) и минимума (172.3), получим выраже­ния для радиуса m-го светлого кольца

r_m=Ö((m-^l/₂)l₀R)    (m=1, 2, 3,...)

и радиуса m-го темного кольца

Измеряя радиусы соответствующих колец, мож­но (зная радиус кривизны линзы R) определить l₀  и, наоборот, по известной l₀ найти радиус кривизны линзы R.

Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны l₀  (см. (174.2)). Поэтому система светлых и темных полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относитель­но друга полос, образованных лучами раз­ных длин волн, и интерференционная кар­тина приобретает радужную окраску. Все рассуждения были проведены для отра­женного света. Интерференцию можно на­блюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отра­женного света отличатся на l₀/2, т. е. мак­симумам интерференции в отраженном свете соответствуют минимумы в проходя­щем, и наоборот.